The notion of Month and Week reaches back to pre-historic times. The Month was a 30-day moon cycle. A Week was a phase of the moon cycle: the new moon, the first quarter moon, the full moon, or the third quarter moon. Thus a week was seven days. It was also the number of the known heavenly bodies. The week became the natural timeframe for humans: six days of work, and a day of rest.
The history behind the weekday names and their sequence is mind-boggling.
We know that the weekday names are linked to heavenly bodies, the sun, the moon, and the known planets. This is particularly evident in the Roman languages, like Latin and French. In English and German, some weekday names relate to deities associated with these same celestial bodies.
Each weekday stands for a celestial object in the sky. But the names seem set in random order. Why is Tuesday (Mars) before Wednesday (Mercury)? One day is like the other. There is nothing that sets them apart, not like the meaningfully named seasons.
So, how did ancient civilizations assign the day names in today's universally established order? The answer is truly eye-opening. Stay with it; it is a long read.
In ancient times, only seven heavenly bodies were known and revered. Each was given a name. The planets Uranus and Neptune had yet to be discovered. Each of the seven objects was sacred, and each was an embodiment of a God or Goddess. Each new day was devoted to a celestial object in a seven-day rotation.The seven heavenly objects have traditionally been listed in the order of the length of their orbit, meaning the elapsed time before their reappearance. In ancient times, the Earth was the center of the universe, and the sun was believed to circle the Earth once a year. Here is how long it takes for each to complete an orbit:
1. Moon: 29 days, Dies Lunae, Monday
2. Mercury: 88 days, Dies Mercurii, Germanic God Wodan, Wednesday
3. Venus: 225 days, Dies Veneris, Germanic Goddess Frigg, Friday
4. Sun (using the earth cycle: 1 year, Dies Solis, Sunday
5. Mars: 2 years, Dies Martis, Germanic God Tiw, Tuesday
6. Jupiter: 12 years, Dies Iovis, Germanic God Thor, Thursday
7. Saturn: 29 years, Dies Saturni, Saturday
So, we should think that the lineup of the days would be as follows:
Monday,
Wednesday,
Friday,
Sunday,
Tuesday,
Thursday,
Saturday
or in reverse.
But it is not ...
Let us dig into it further. As early as four or five thousand years ago, the ancient Egyptians and Babylonians already split the day into time sections, a 12-hour day and a 12-hour night, a total of 24 hours. Time devices, such as shadow clocks, marked the hours as the sun ascended in the morning and descended in the evening, also allowing for the twilight hours. The number 12 has always been important; finger-bone counting may have been its origin.
In ancient Egypt and other civilized countries, each new hour was dedicated to a God. So, 24 times each day, until midnight, in rotation, at the turn of the hour, the hour was devoted to another God, in strict order of the orbital lineup. The hour after midnight was paramount. The God of the first hour after midnight owned the whole new day, and the day was named after that hour's deity.
There were only 7 God Stars, so every seven hours, the cycle repeats itself. But there are 24 hours in a day. The number 7 does not neatly divide into 24; there is a remainder of 3. Thus, every midnight, every 24 hours, the pick from the fixed list of Gods shifts forward by an extra 3. The animated GIF below explains it better. Watch it, and be patient; it runs for a minute. It is amazing! The seven-day, 24-hour run-through creates the exact day order we know today: Monday, Tuesday, Wednesday, Thursday, Friday, Saturday, and Sunday.
We all know the value of Pi, the ratio of a circle's circumference to its diameter: 3.14. We confidently use that 3.14 number in circles and spheres calculations. But have you ever tried calculating that number to a 10-decimal accuracy? Are you wondering how the Babylonians figured it out and calculated Pi almost 2500 years ago and how Archimedes and Euclid refined and proofed the theorem? With some basic knowledge of the Pythagorean theorem learned in Grade Six, we calculate the Pi value easily. And it is fun.
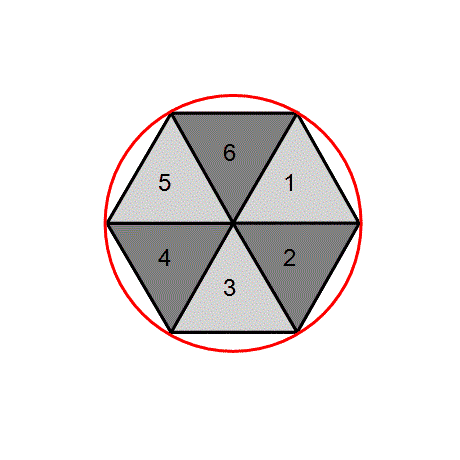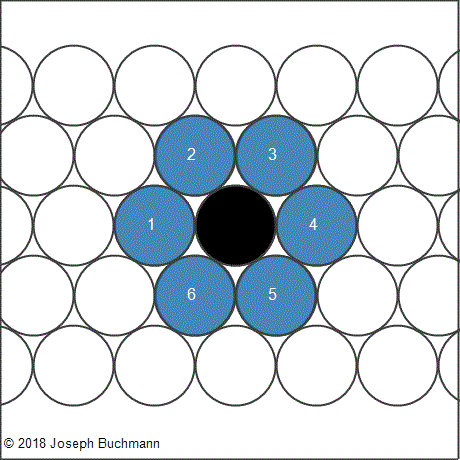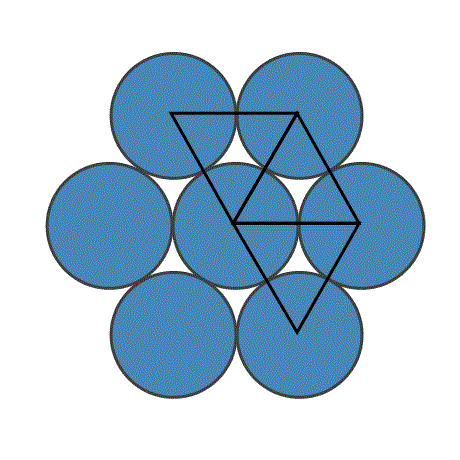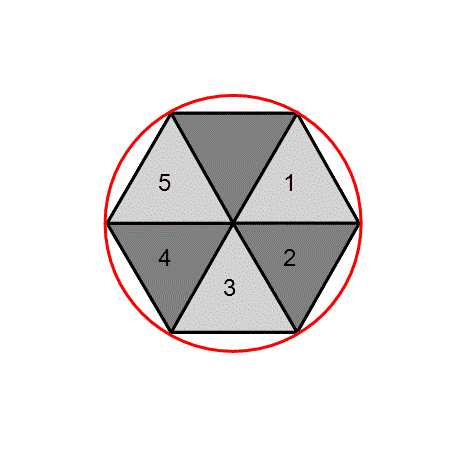The realization that six circles fit perfectly around a single same-size circle must have been thought-provoking to ancient mathematicians, and it opened up a new world of geometry. They realized that it was the core of the hexagon. The Hexagon, as the name implies, is a six-sided polygon, all sides of equal length. It is a fundamental figure. Even Nature uses it; think of the honeycomb. Here, Nature meets Mathematics. The hexagon encaptures six equilateral triangles, each triangle side equal to the length of the hexagon sides - and is the hexagon's radius. The hexagon is the perfect base for our Pi calculation.
Demonstrating it differently, we place six cans of beer around a same-size can. They fit perfectly. Then, mentally draw lines from the center of each can to the center of each neighboring can, thus three lines emanating from each can. The drawing is a hexagon with six perfect triangles.
The hexagon is a quasi-circle. The ratio of the circumference of that 'circle' (six triangle sides) to its diameter (two triangle sides) is 3. It is the beginning point of our Pi calculation.
We start with a triangle of the hexagon. Running through several iterations, we slice the triangle in half, again and again, aligning the slices to the hexagon's imaginary 'circle' line. Cutting a triangle in half creates two triangles, each with a 90-degree angle. This allows us to use the Pythagorean theorem. The pictures below show the process in more detail. As the number of triangles doubles with each iteration, from 6 to 12, 24, 48, etc, the imaginary outer rim becomes rounder and rounder, smoother and smoother. After only ten iterations, the original hexagon has over 6,000 edges and appears virtually round to the eye. The circle's circumference divided by the diameter (double-radius) gives us the new Pi ratio. The circle will never be completely round, and the Pi number can thus be calculated to infinity.
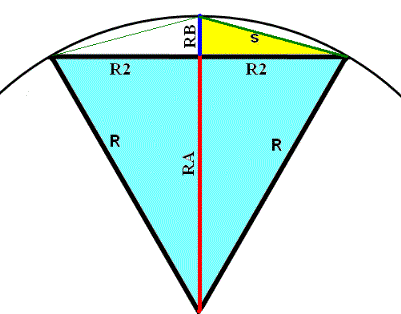We cut the first equilateral triangle in half. Between the two halves, we draw an imaginary line from the center of the circle, a length equal to a side of the original triangle (the radius), shown as the combined red RA and blue RB lines in the illustration, crossing the upper side of the triangle (R2). The line RA+RB is equal to line R. We must now calculate the length of the red RA line and the length of the blue RB line. Here, we do our first simple Pythagoras calculation. R is the radius, and R2 is half of the radius). RA can be calculated as follows:
RA = Square Root of ((R*R) - (R2 * R2))
Now that we know the value of RA, we calculate the value of RB, by deducting the RA from the value of the radius. RB = R-RAWe are now ready to refine the circle line further. The initial six sides will be doubled to 12. With our second Pythagoras calculation, we obtain the hypotenuse of the yellow RB and R2 configuration, shown as a green line (S) in the image. The calculation is as follows:
S = Square Root of (( R2*R2) + (RB*RB))
With this calculation, we now have 12 equal sections around our circle, and the Pi stands much improved at 3.13. It is better, but it is not good enough.
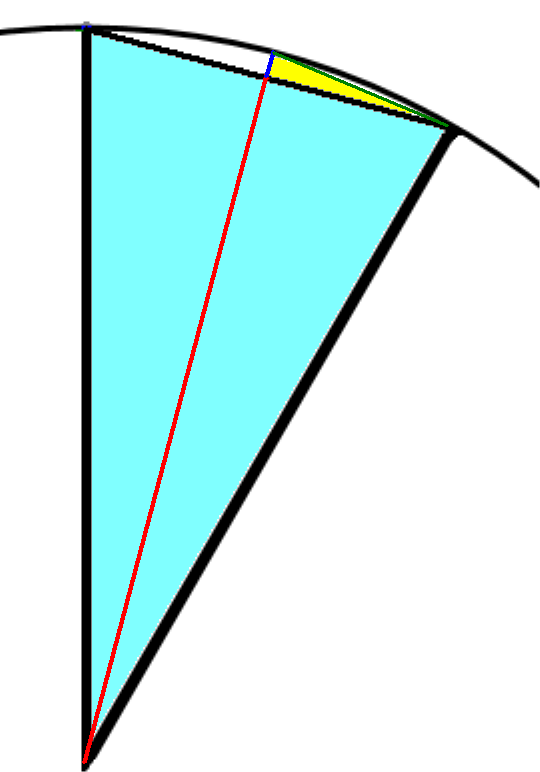And we continue. Following the same steps, we cut the new triangle in half and re-calculate. We repeat it over and over. The radius (R) remains the same, but the R2 is 1/2 of the previous line S. The Pi improves to 3.139, then 3.141. Once we reach 20 iterations, we have a near-perfect Pi value of 3.14159265358976.
We can calculate it to infinity. Each iteration gets closer to the ultimate Pi number, unreachable because the circle is never completely round.
Some more interesting facts.....
A full circle is expressed as 360 degrees. The popular belief is that the number 360 is based on the number of days of the solar cycle, each day representing one degree. The Sumerians and Babylonians of Mesopotamia used the Sexagesimal numbering system (Base-60). Since a circle is mathematically closely related to a hexagon, there can be an argument that 360 degrees represents the six sides, each with the sexagesimal value of 60.
The Sumerians and Babylonians practiced finger-bone counting. With an open hand, using the thumb, they tapped and counted the finger-bones; four fingers, each with three bones, a count of 12. The other hand tracked the counts of 12, for example, 5 x 12, a total of 60.
The finger-bone counting method is likely the foundation of the Sexagesimal (base 60) numbering system used by the Sumerians and Babylonians, a system still used today when referring to degrees, minutes, and seconds. The high divisibility of the number 60 makes it very special. You can divide the number by 2, 3, 4, 5, 6, and more.
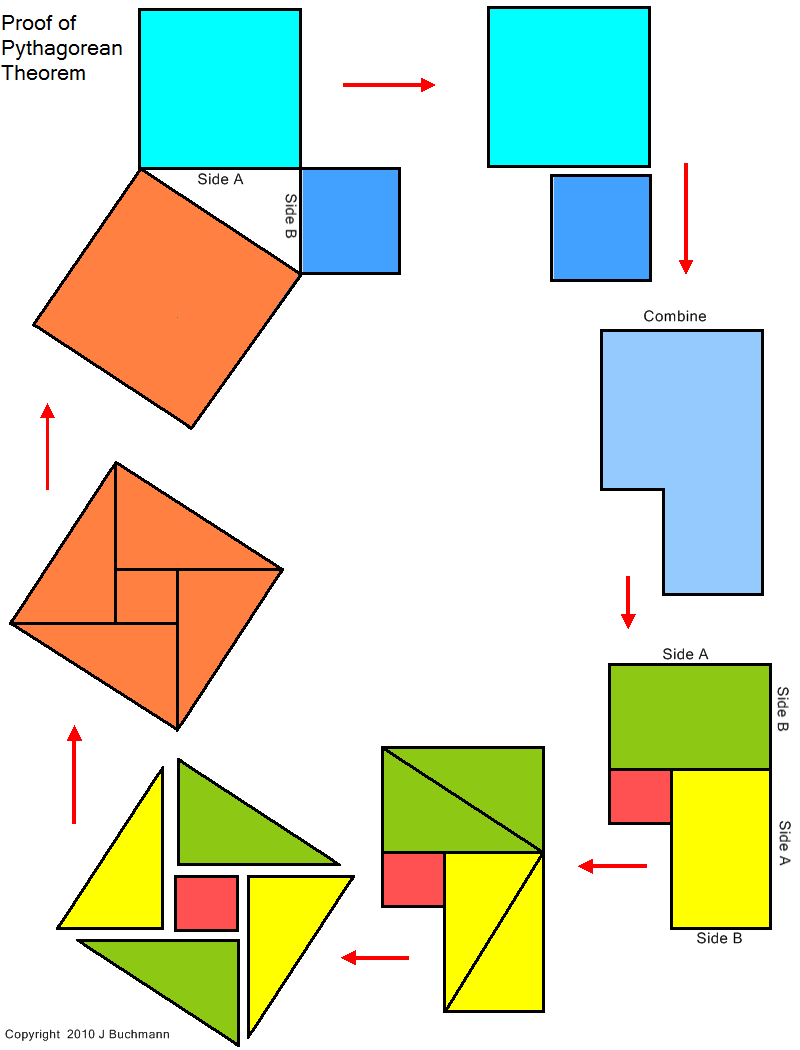
Here is a simple presentation that proves the Pythagorean Theorem.
The 'Golden Ratio' is one of the most compelling curiosities in nature. It is the space where the law of nature harmonizes with the rules of mathematics and physics. No wonder it is also called the divine proportion and the golden number.
In mathematics and the arts, a rectangle has a golden ratio if the ratio of the longer side to its shorter side is the same as the ratio of the total of both sides to the longer side. An object created by man or nature, built to a golden ratio, is of the optimum beauty to the human eye. Early artists and architects were aware of the importance of the golden ratio. The architectural design of the Parthenon in Athens has many elements that follow the rules of the golden ratio, by instinct or by calculation. Most books printed in the 16th to the 18th century had heights and widths in harmony with the golden ratio, accurate to within a tenth of an inch. The Mona Lisa painting has Ratio dimensions. The divine proportion of the rectangles gives the artwork the most appealing and pleasing appearance.
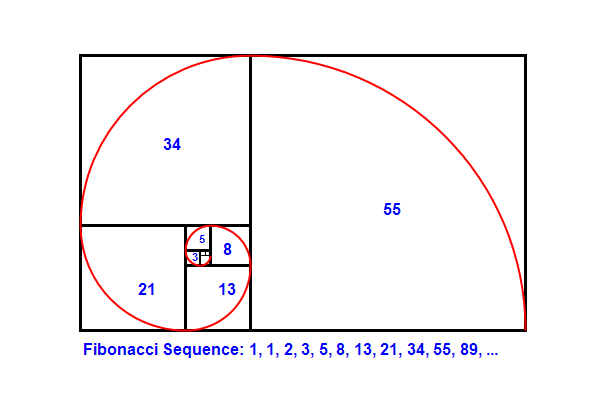
The Fibonacci Sequence is a progression of numbers where each number is the total of the two preceding numbers.
1
2
1+1 = 3
2 + 3 = 5
3 + 5 = 8
5 + 8 = 13
8 + 13 = 21
13 + 21 = 34
21 + 34 = 55
...
...
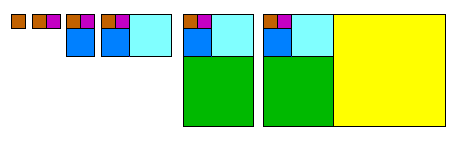
The Fibonacci Sequence can also be demonstrated by a build of square boxes or by drawing a snake. In the example, the ratio of the last set of numbers (34/21) is 1.619... As the Fibonacci Sequence increases, the ratio gets closer and closer to the Golden Ratio of 1.61803399..., but never exceeds it. The ratio is an irrational number; it is never exhausted.
It is fascinating to find Fibonacci numbers everywhere in nature. These numbers are nature's way of tallying things. We have eight teeth on each side (two incisors, one canine, and five molars). We have five fingers on each hand and five toes on each foot. Petals in flowers, seeds on flower heads, and spirals in sunflowers almost always match Fibonacci numbers. Shrimps have five pairs of walking legs and five pairs of swimmerets. Starfish have five arms. Check the joints, the bones, in your fingers. They are aligned in a Fibonacci sequence, the length of each increasing by the golden ratio factor of 1.61. Some flowers do have four or six petals. Oh, you say, these are not Fibonacci numbers. But look closely; you will see that the petals may be in two layers, each matching a Fibonacci number. There are exceptions. The probability of a four-leaf clover is 1 in 10,000. No wonder finding one is considered good luck.
The value of the golden ratio is 1.618033... and can also be calculated by taking the square root of 5, adding 1, and dividing the result by 2. Or, as mentioned before, pick a number from the Fibonacci Sequence and divide it by the next lower value in the sequence.
In the early years of the Romans, the year started with March and consisted of only ten months. After ten named months, there was a nameless two-moon dead winter season. March, the first month of the year, was named after Mars, the God of Wars, aptly named for the month when the soggy soil firmed up, daylight grew longer, and young men were called back to fight and conquer new lands and bring home the booty. The origin of April is Aprilis, meaning 'the month that opens,' perhaps alluding to the buds opening up in spring. It has been argued also that April may be named in honor of Aphrodite, the Goddess of Love and Beauty. May and June were probably named after the Roman Goddesses Maiesta and Juno. The remaining six months were named after their respective numeric position. Remember, March was the first month. So, Quintilis (July) was the name of the fifth month, Sextilis (August) the sixth month, then Septilis, Octilis, and on, referring to Roman numbers.
A month represents a moon cycle. The moon cycles do not calibrate neatly into a 'sun' year. Twelve moon cycles represent about 354 days; a solar cycle is just over 365 days. Over the long span of history, different approaches were used to handle the discrepancy.
Illogically, the residual leap-year days are adjusted in February instead of December. Why? With the 30-day and 31-day months orderly alternating, why is there an exception for July and August? Why is September the ninth month when the number Seven is in its name, like 'Septem' in Latin? And the same for October, November, and December. There are valid explanations for all these questions.
Around 700 BC, the Romans added the two 'dead' winter moon cycles at the beginning of the calendar year. Januarius was named after Janus, God of Gates, Lord of Beginning and End, his head appropriately depicted with two faces looking in opposite directions, looking back at the old year and looking forward to the new year. Februarius refers to Februa, the festival of purification celebrated in Rome that month. A root word for Februa refers to 'burning,' perhaps relating to fever. It makes sense; we all get a cold or the flu when our defenses are down after a long winter. Adding the two months in front explains why the names of September to December are now out of whack with their embedded sequence number.
The number of days allocated to the months varied. The Romans viewed odd numbers as more propitious than even numbers. An odd number felt more copious because there was some extra after an equal sharing. The left-over or deficit days were handled somehow but were eventually taken care of in February, the end of the original dead season. Still today, February is the handler of the adjustment days.
Then, Roman Emperors with big egos arrived on stage. Julius Caesar wanted a month named after him. He ordered that Quintilis, the fifth month, be named July. Not to be outdone, Emperor Augustus claimed the sixth-month Sextilis for him. Julius' month traditionally had 31 days, but Augustus' month Sextilis had 30 days. It was unacceptable for Augustus to have a month with fewer and less favorable days than his uncle Julius, so the number of days in August was increased to 31, and it still is today.
Decades ago, the Europeans developed and propagated paper sizes based on the 'Square Root of Two' ratio, now also dubbed the Lichtenberg ratio. It follows the widely used Metric system. The ingenuity of the v2 ratio is that when the paper is cut or folded in half lengthwise, the two halves have the same aspect ratio as their parent.
The scheme has three series, the 'A' series being the most prevalent. Thus, the paper size A0 has a total area of 1 square Meter. The Height to Width ratio is 1.4142 (the square root of 2). When you cut the A0 paper sheet in half horizontally, you have two A1 size sheets, when rotated, both with the width-height ratio as the original A0. The A1 cut in half again creates two A2 sheets, then two A3 sheets, then A4s, and so on. The A4 is the most commonly used paper size, the equivalent of the North American Letter Size. The thought behind the ratio is ingenious; it challenges the human mind.
